ENCOR 350-401|Часть 3.1 - Shortest path algorithms, Path selection
ENCOR 
Приветствую, друг!
Очередной многобуквенный выпуск, ибо я еще не придумал другого варианта представления контента. Но это в процессе!
Сегодня у нас еще одна остановка перед погружением в протоколы динамической маршрутизации - виды алгоритмов, которые используются для выбора оптимального пути и сопутствующие сущности, принимающие активное участие в этом процессе.
Сегодня в программе
- About graphs
- Distance vector
- Link-state
- Enchanced Distance Vector
- Path vector
- Path Selection
- Sources
About graphs
Протоколы динамической маршрутизации делятся на IGP - обмен маршрутной информацией в рамках одной AS и EGP - обмен маршрутной информацией между AS.
Всех представителей вы уже точно знаете:
IGP: RIPv2, OSPFv2/v3, ISIS, EIGRP
EGP: BGPv4
В основе работы протоколов лежат алгоритмы, основанные на взаимодействиях с графами.
Любую топологию можно представить в виде графа - это некоторая топологическая модель, абстракция, позволяющая представить набор маршрутизаторов - вершинами, а подключения между ними - ребрами.
Граф - пара множеств (V, E), где V - множество вершин (Vertex), а E - множество неупорядоченных пар этих вершин V, принадлежащих V, т.е ребер (Edge). Графы бывают разные, нас интересует взвешенный неориентированный граф:
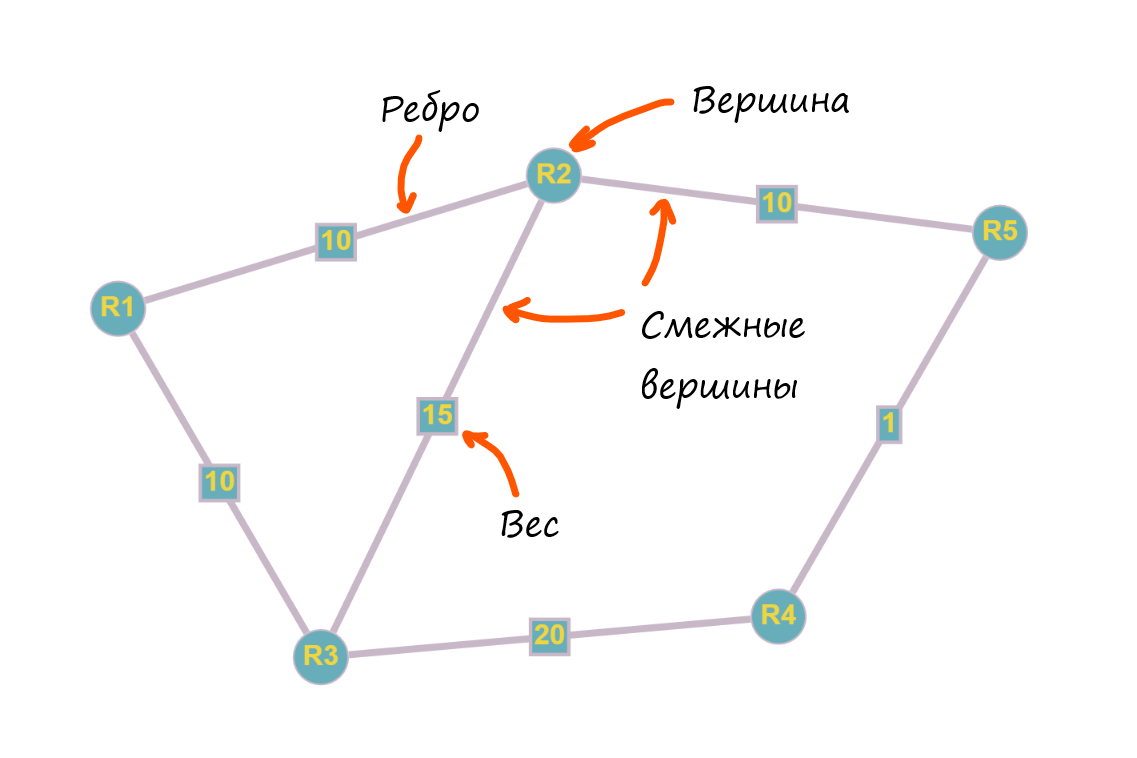
Ребра могут иметь вес (стоимость), которая может быть как отрицательной, так и положительной. Такой граф называется взвешенным.
Неориентированный означает, что у нас не определено направление для ребер.
Графы - обширное поле для применения различных алгоритмов. Нахождение маршрута от одного объекта к другому, поиск связанных компонент, вычисление кратчайших путей, поиск сети максимального потока и многое другое.
Найти самый оптимальный маршрут в имеющейся топологии и рассказать об этом соседям - основная задача протоколов динамической маршрутизации. В теории графов эта задача называется - поиск кратчайшего пути и для ее решения используются алгоритмы поиска кратчайшего пути.
Как можно догадаться по названию, алгоритмы поиска кратчайшего пути находят пути между двумя вершинами в графе, такие, что общая сумма весов составляющих ребер минимальна.
Мы посмотрим на такие алгоритмы как:
- алгоритм Беллмана-Форда
- алгоритм Дейкстры
- алгоритм DUAL
Небольшой дисклеймер для тех, кто сразу решил стать связистом и пошел учиться по профилю и набрел на эту статью. Я не настоящий сварщик и только учусь. Поэтому для меня дискретная математика, теория графов и прочие прелести - в новинку. Я о них знал, но дальше общего смысла разбираться не лез. Если в тексте вы нашли неточности, не стесняйтесь на это указывать. Проще всего это сделать в Телеграм-группе.
Смотреть на алгоритмы мы будем с точки зрения их применения в семействах протоколов динамической маршрутизации:
- Distance vector (DV)
- Link-State (LS)
- Enchanced Distance vector (eDV)
- Path vector (PV)
Спойлер: Дейкстру попробуем разобраться чуть подробнее. Почему такие лавры? В силу его важности и популярности.
Distance vector
Distance vector (DV) протоколы, такие как RIP, анонсируют маршруты как векторы с указанием дистанции до узла, где дистанция — это стоимость, такая как количество переходов (hop count), а вектор — это IP-адрес маршрутизатора следующего перехода (next-hop), используемый для достижения пункта назначения.
Как работает DV алгоритм в общем:
- Маршрутизатор передает свой вектор расстояния каждому из своих соседей в пакете маршрутизации.
- Каждый маршрутизатор получает и сохраняет последний полученный вектор расстояния от каждого из своих соседей.
- Маршрутизатор пересчитывает свой вектор расстояния, когда:
- Он получает вектор расстояния от соседа, содержащий другую информацию, чем раньше.
- Он обнаруживает, что линк до соседа более недоступен.
Задача, которую алгоритм решает на шаге 3 - как раз и есть нахождение кратчайшего пути между вершинами графа.
Суть задачи заключается в обсчете графа и делать это можно по разному. В случае DV, самая явная аналогия - маршрутные знаки на перекрестках. Если ваш навигатор не работает и нет карты, вы доверитесь указателю на знаке, например “Москва 10км ->”. В данном случае Москва - это вектор, а 10км - стоимость.
После расчета, кратчайший маршрут инсталлируется в RIB и анонсируется соседям.
DV снисходительнее к вычислительным мощностям CPU т.к нет необходимости обсчитывать всю топологию сети, достаточно лишь знать, что некоторый кусок сети находится за соседом.
Недостатками можно считать медленную сходимость после аварии, возможные кратковременные петли, проблема счета до бесконечности (count to infinity).
Итого:
- каждый маршрутизатор вычисляет расстояние между собой и каждым возможным пунктом назначения, то есть своими непосредственными соседями.
- маршрутизатор не хранит всю топологию сети, а делится своими знаниями о своем кусочке сети со своими соседями и соответственно обновляет таблицу на основе своих соседей.
- обмен информацией с соседями происходит через равные промежутки времени.
- использует алгоритм Беллмана-Форда для создания таблиц маршрутизации
- RIPv2 - полуживой представитель в настоящее время
Bellman-Ford’s algorithm
В основе работы DV лежит алгоритм Беллмана-Форда - находит кратчайшие пути в графе (с отрицательными или положительными весами) от исходной вершины до всех остальных.
Алгоритм Беллмана-Форда бездумно проходит итеративный путь расчета через все рёбра.
Идея: если предположить, что цикл с отрицательным весом отсутствует, если мы вычислили кратчайшие пути с не более чем i ребрами, то итерация по всем ребрам гарантирует получение кратчайшего пути с не более чем (i+1) ребрами.
Изначально значения стоимости до каждой вершины устанавливаются в бесконечность, кроме исходной, расстояние до нее мы точно знаем, оно = 0.
С каждой итерацией алгоритм пытается рассчитать путь до каждого из узлов, что, в конечном итоге, дает кратчайшие маршруты (с наименьшим весом) до нужных узлов.
Алгоритм использует восходящий подход расчета т.е сначала вычисляется кратчайшие расстояния, которые имеют не более одного ребра на пути, затем два, три и так далее.
В RIP вес ребер по умолчанию = 1 т.е технически каждая единица веса = 1 next-hop
На пример подробнее посмотрим, когда доберемся до RIPv2.
Алгоритм не способен обработать петлю, что дает нам возможную проблему, которая называется счетом до бесконечности или count to infinity.
Count to infinity- буквально, узел считает до бесконечности расстояние до узла, в тот момент, когда стала возможна петля маршрутизации. Узел увеличивает свое расстояние до пункта назначения, пока не достигнет предопределенного максимального значения расстояния (если оно есть). (Для этого в RIP существует ограничение на 15 хопов)
Проблема Count to infinity ни что иное как следствие петли. Петли маршрутизации обычно возникают, когда интерфейс выходит из строя или два маршрутизатора одновременно отправляют обновления друг другу. Возникает это по причине того, что оба соседа до этого изучили все сети в топологии и будут делиться этой информацией со всеми соседями через равные промежутки времени.
Когда дойдем до RIP, посмотрим, какими средствами решается проблема петель.
Link-state
Link-state протоколы (LS), можно представить как противоположность DV, который мы представляли по аналогии с дорожным знаком с направлением и указанием стоимости. LS же сравним с навигатором, который прокладывает наилучший путь, основываясь на данных об авариях, пробках, плохой дороге и т.п, вместо того, чтобы ориентироваться только на расстояние от A до B.
Теперь каждый маршрутизатор не делится всей известной маршрутной информацией, а отправляет в соседей кусочки топологической информации. Полноценный обмен всей топологией происходит в момент первичной инициализации протокола.
Для обмена использует специальные пакеты - LSA/LSR, для анонсов и приема кусочков топологии, информация о которых затем хранятся в локальной базе маршрутизатора - LSDB.
В результате обмена такими пакетами, каждый маршрутизатор будет иметь полную картину всей топологии.
Используя полную карту сети, каждый маршрутизатор строит SPT (shortest path tree) граф - дерево кратчайших путей для области с текущим маршрутизатором в качестве корня, используя алгоритм Дейкстры.
После расчета SPT, процесс LS протокола заполняет таблицу маршрутизации наилучшими маршрутами до каждой из сетей, подпадающих под конфигурацию.
Итого:
- расчет производится на основе полной топологии сети, а не на отдельных его участках
- маршрутизаторы обмениваются кусочками топологии, вместо отдельных маршрутов
- обмен происходит с помощью специальных сообщений
- имеет место установление соседств между маршрутизаторами, чтобы синхронизировать текущие состояния т.к каждый маршрутизатор должен отчитаться, что имеет актуальную информацию о топологии
- используется алгоритм Дейкстры
- На сегодняшний день у нас есть два представителя этого семейства:
- OSPF
- IS-IS
Dijkstra’s algorithm

Эдсгер Дейкстра был крайне интересный мужик, вряд ли вы читали его биографию, поэтому вот несколько примечательных фактов о:
- работал над созданием ЭВМ X1. Эта машина была создана тремя энтузиастами за год.
- именно для оптимизации разводки плат для X1 Дейкстра придумал свой алгоритм поиска кратчайшего пути, который ныне называют “Алгоритм Дейкстры”
- лауреат премии Тюринга (самая престижная награда по информатике)
- был программистом, до того как это стало мейнстримом (в 60-х “программист” еще не звучало гордо)
- является одним из авторов структурного программирования (вот эти наши современные наследования, циклы, ветвления)
- на спор создал компилятор Алгол-60 для языка Алгол, который позиционировался как замена FORTRAN (Дейкстра презирал FORTRAN)
- автор множества заметок, публикаций и книг, охватывающих широкий спектр тем
Статьи, которые Дейкстра именовал как EWDX (EWD - инициалы, X - порядковый номер) собраны в [манускрипте](https://www.cs.utexas.edu/~EWD/.
Но вернемся к алгоритму Дейкстры, который Эдсгер Дейкстра изобрел в 1959 году. Ну как изобрел, придумал в кафе за 20 мин. Алгоритм выполняет ту же задачу, что и алгоритм Беллмана-Форда, но иначе работает с графом.
Алгоритм Дейкстры, на мой взгляд, важнее для понимания, чем Беллмана-Форда, поэтому я попробую рассмотреть его работу на примере наглядной топологии:
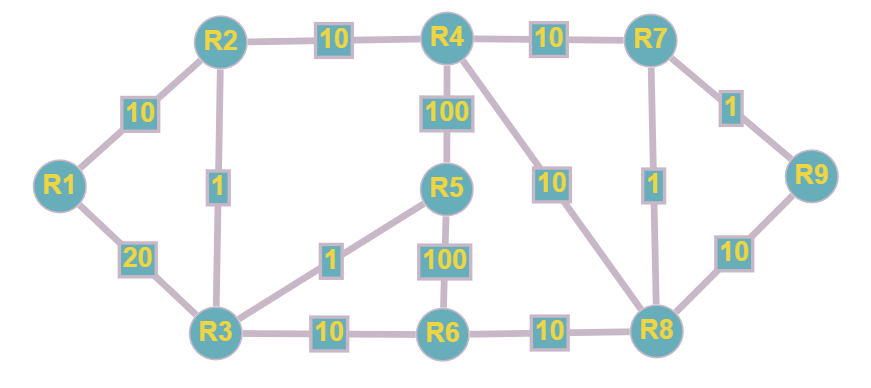
У нас есть множество вершин V {R1…R9} и множество ребер E, каждое из которых имеет положительное значение веса (стоимости.).
Задача: Найти кратчайшие пути до всех вершин из вершины R1 - это наш корень.
Нам понадобится две структуры данных: массив, в котором будем хранить значения стоимостей по мере их вычисления и очередь, куда будут попадать вершины, для которых еще возможно провести поиск в ширину (BFS).
Итак, R1 будет вершиной-источником (корнем дерева) и его стоимость будет = 0 т.к чтобы добраться до самого себя, не нужно никуда ходить :)
Шаг 0: При этом, все остальные стоимости будут = бесконечности (INF) т.к в начале расчета мы ничего об этих расстояниях не знаем.
Сейчас ситуация выглядит как на картинке ниже:
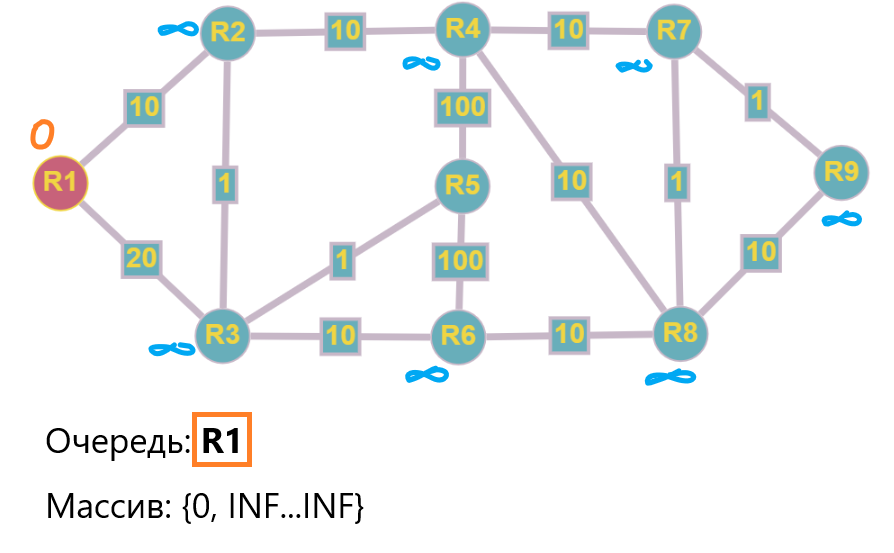
В очередь будут попадать те вершины, для которых будет выполнено обновление текущего значения расстояния. Новые вершины я буду помечать зеленым, те, что забираются из очереди, буду зачеркивать.
Шаг за шагом алгоритм будет забирать и добавлять узелы в очередь и выполнять, по сути, поиск в ширину по графу т.е рассчитывать стоимость до каждой из смежных вершин. Затем обновлять стоимости до узла, если его новое значение стоимости оказалось < текущего значения. В том числе и в сторону лучшего пути, а то вдруг там что-то поменялось :)
Шаг 1: Забираем R1 из очереди, от нее у нас две смежные вершины: R2 и R3, для них обновляем значения стоимостей т.к 10 и 20 < INF. Добавляем R2 и R3 в очередь.
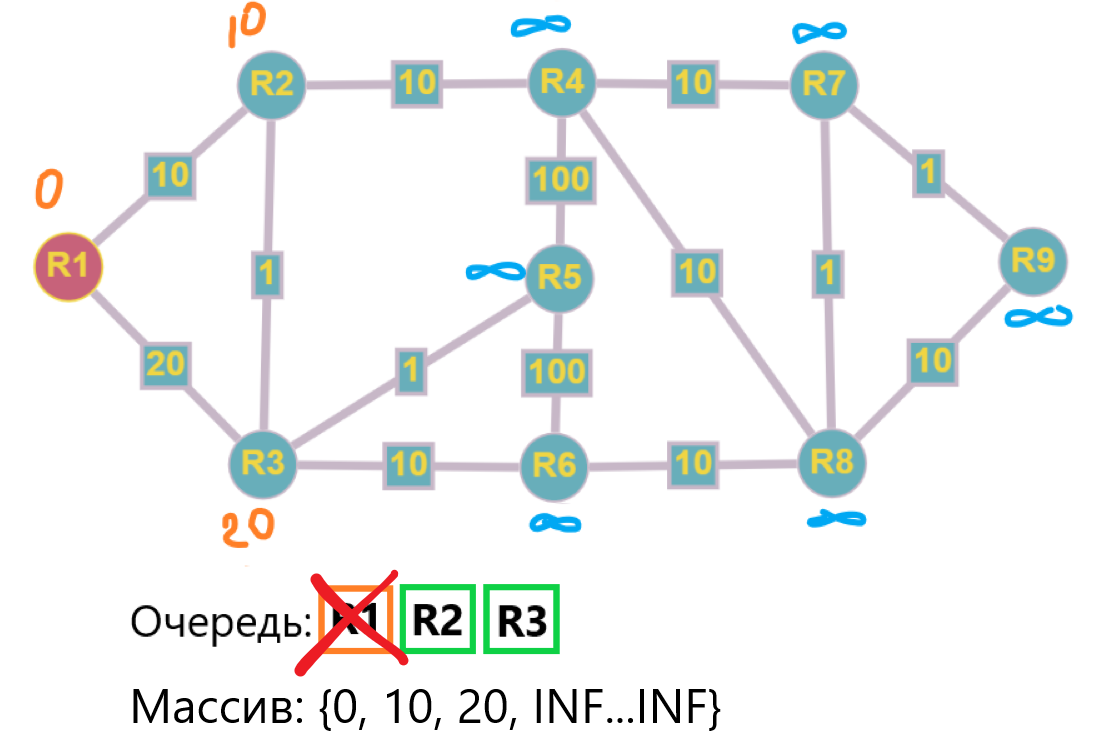
Шаг 2: Берем из очереди R2 (по порядку) и обновляем стоимости смежных узлов:
- R1 остается без изменений т.к 10 > 0
- значение для R3 обновляется т.к 11 < INF, R3 добавляется в очередь (обратите внимание, уже повторно)
- R4 обновляется т.к 20 < INF, R4 добавляется в очередь
Смежные узлы обработаны, а очередь покинул уже второй узел - R2.
В массив, напомню, на протяжении всего цикла, записываются значения стоимостей.
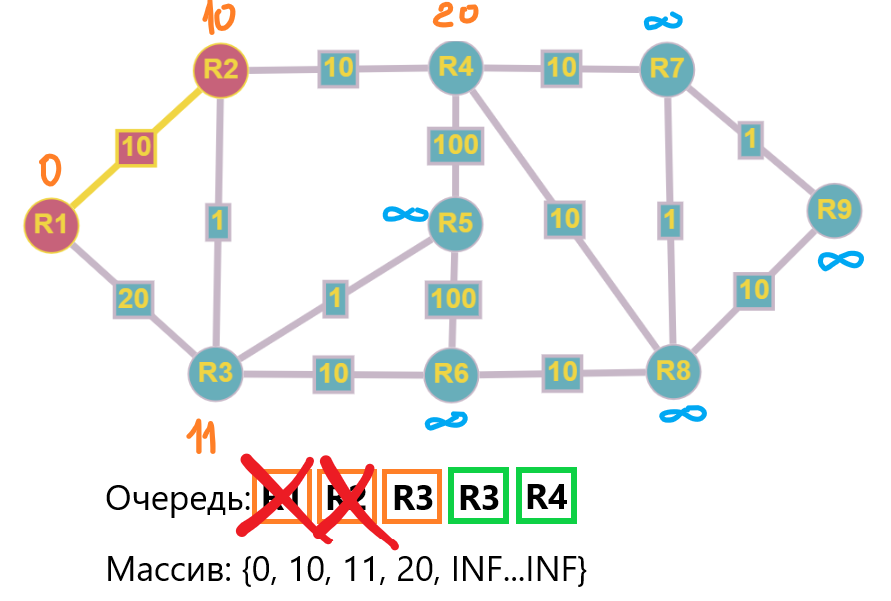
Шаг 3: Продолжаем цикл, берем R3 из очереди и обрабатываем значения:
- R1: ничего не изменится, нет значения, которое будет меньше 0, граф у нас строго с положительными весами, это требование алгоритма Дейкстры
- R2: 11 + 1 = 12 > 10, без изменений
- R5: 11 + 1 = 12 < INF, обновляем значение и добавляем R5 в очередь
- R6: 11 + 10 = 21 < INF, обновляем значение и добавляем R6 в очередь
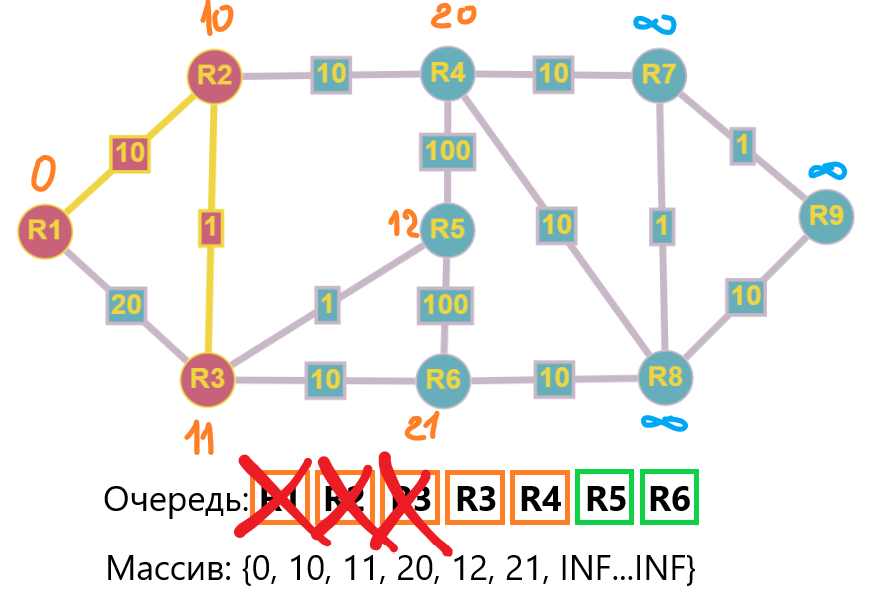
Смежные узлы обработаны, R3 покидает очередь. Сейчас у нас получилась ситуация, когда R3 встречается повторно. В этом случае расчет будет “холостым” т.к условие должно удовлетворять именно <, а не <=. Проворачиваем все те же действия, забираем R3 из очереди, обрабатываем смежные вершины и переходим к следующему шагу.
Алгоритм Дейкстры может быть решен через приоретизированую очередь, тогда в очередь не будут попадать несколько одинаковых улов (как это получилось выше). Т.е узлы с меньшей стоимостью будут иметь приоритет при расчете (располагаться левее в очереди). В данном примере показана грязная очередь.
Шаг 4: Забираем R4 из очереди и обрабатываем значения:
- R5 без изменений, 20 + 100 = 120 > 12
- R7 20 + 10 = 30, обновляем значение и добавляем R7 в очередь
- R8 20 + 10 = 30, обновляем значение и добавляем R8 в очередь
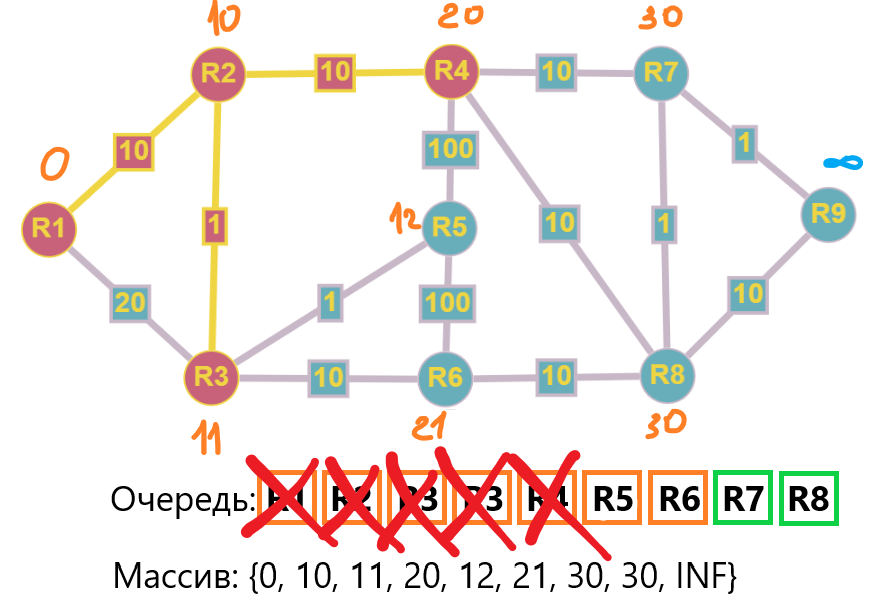
Продолжая циклически обрабатывать узлы, мы получим следующую картину:
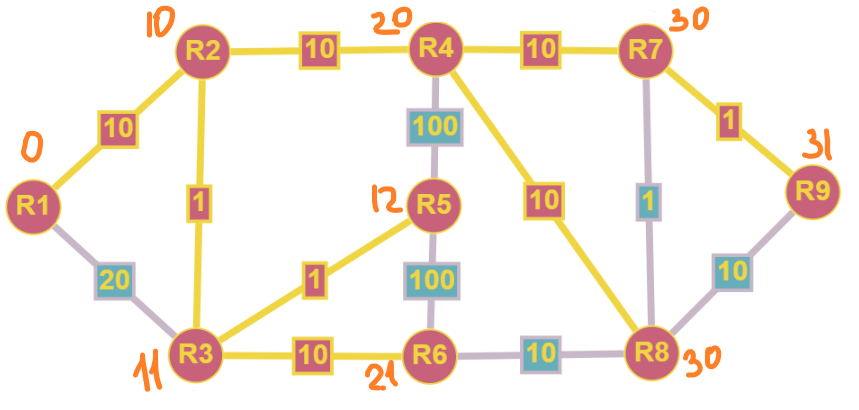
В виде дерева это будет выглядеть так:
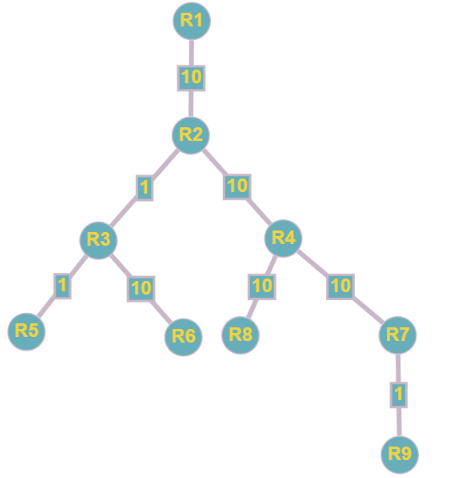
Так же мы получили законченный массив, который содержит в себе значения минимального расстояния до каждой из вершин графа.
{0, 10, 11, 20, 12, 21, 30, 30, 31}
Еще один вариант решения, который проще для первоначального объяснения работы алгоритма, заключается в выборе наименьшего расстояния для каждой из вершин, которые еще не являются частью SPT. Так же идем поиском в ширину для смежных вершин, но выбираем узел с наименьшим расстоянием - это и будет часть нового SPT множества.
Идея: обходим граф в ширину, пересчитывая оценку расстояния от источника до других вершин. Жадный принцип – продвижение по ребрам с меньшим весом.
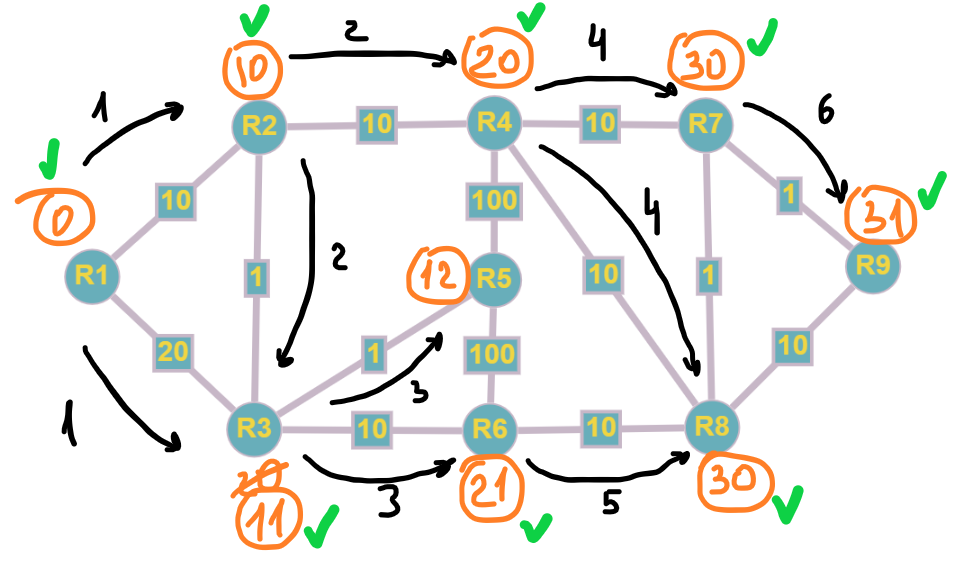
За 6 шагов мы нашли те же самые значения, придерживаясь правила наименьшего расстояния.
Согласитесь, после рассмотрения наглядного примера, алгоритм достаточно прост. Но мы еще не ответили на вопрос, чем же алгоритм Дейкстры отличается от алгоритма Беллмана-Форда.
Dijkstra’s vs Bellman-Ford’s
Алгоритм Дейкстры похож по принципу работы на Беллмана-Форда. Оба являются single-source shortest path algorithm, что значит поиск кратчайшего пути через вершину-источник. Но если они похожи, зачем в OSPF используется Дейкстра, а в RIPv2 Беллман-Форд? Попробуем разобраться, сильно не вникая в математику.
Основное отличие - разный подход к обсчету графа - Дейкстра строит “обдуманно” граф-дерево с кратчайшими путями до всех нод в топологии, а беллман-форд строит то же дерево, но использует подход динамического программирования т.е “тупо” итеративно проводит расчет пути до нод с одного ребра и далее по возрастающей проходит по всем вершинам графа, считая и обновляя стоимости на каждой итерации.
Динамическое программирование - решение задачи находится путем комбинирования решений более простых подзадач.
Стоит так же отметить, что алгоритму Дейкстры скармливается вся топология, а Беллман-Форд считается асинхронно на каждом маршрутизаторе в отдельности.
Из предыдущих выводов следует, что Дейкстра лишен проблемы count to infinity и, следовательно, петель, что влияет на время сходимости.
В интернетах вы найдете утверждение, что Дейкстра не умеет в отрицательные веса (т.е требует, чтобы веса ребер графа были положительны или он не будет работать). А Беллман-Форд наоборот умеет учитывать отрицательные веса и даже находить отрицательные циклы, когда стоимость может быть бесконечно уменьшена и краткий путь не будет найден.
Но какой смысл этого отличия, если в сетях не может быть отрицательных весов? Я не умею в дискретную математику, поэтому предположу только, что этот нюанс влияет на скорость обсчета т.к не нужно закладываться в коде на отрицательные циклы. Иными словами, это обстоятельство, в том числе, определяет принцип работы алгоритмов и влияет на время их работы. Т.е итеративный принцип работы Беллмана-Форда как раз и позволяет ему работать с отрицательными весами, жертвуя временем.
Алгоритмы имеют разные time complexity (или асимптотическая сложность алгоритма), т.е имеют разную временную сложность.
Алгоритм Беллмана-Форда работает медленнее, чем алгоритм Дейкстры. Временная сложность алгоритма Беллмана-Форда составляет O(VE), где V - количество вершин в графе, а E - количество ребер. Это означает, что время выполнения алгоритма Беллмана-Форда растет линейно с увеличением числа вершин и ребер в графе.
Временная сложность алгоритма Дейкстры составляет O(E logV). Это означает, что время выполнения алгоритма Дейкстры растет логарифмически с увеличением числа вершин и ребер в графе, что делает его более эффективным для больших графов.
При увеличении размера входных данных, время выполнения линейного алгоритма будет возрастать гораздо быстрее, чем время выполнения логарифмического алгоритма.
Enchanced Distance Vector
К Enchanced Distance Vector (eDVR) относят EIGRP, который лишен некоторых явных недостатков DV. Например из самых явных отличий:
- не отправляет каждые 30 сек. всю маршрутную информацию соседям, вне зависимости от ситуации т.е использует инкрементальные обновления
- берет в расчет больше параметров для расчета метрики, чем количество хопов до соседа
- использует в основе алгоритм DUAL
- обменивается Hello сообщениями и устанавливает соседства! Прям как LS протокол!
C точки зрения маркетинга, его к отдельной касте протоколов относит сама Cisco, что естественно. Однако EIGRP - классический DV, но немного под стероидами.
По умолчанию EIGRP анонсирует общую задержку (delay) пути и минимальную пропускную способность (minimal bandwith) для маршрута. Эта информация передается во всех направлениях, как это происходит в DV, однако каждый маршрутизатор может вычислить лучший путь на основе информации, предоставленной его непосредственными соседями.
Основу EIGRP, как я уже упомянул выше, составил алгоритм DUAL, работа которого основана на diffusing computations или “распределенные вычисления”. Работает это так: часть информации обрабатывается на каждом узле, затем эта (уже актуальная) информация передается между соседями, для принятия маршрутных решений.
На первый взгляд сложно, но давайте попробуем разобраться.
DUAL algorithm
Принципиально отличается от алгоритмов Беллмана-Форда и Дейкстры т.к был придуман как некоторый ответ на проблемы в существующих алгоритмах.
С одной стороны DV, с его петлями и count to infinity, с другой LS с необходимостью поддерживать полную карту топологии на каждом узле, что влечет за собой затраты ресурсов. В том числе, даже LS не обещал полное отсутствие петель.
В том же OSPF проблема петель “решена” через Backbone Area, к которой должны быть подключены не Area 0 зоны.
Новое семейство алгоритмов представлялось как loop-free и вообще все из себя красивые и продвинутые. Алгоритм появился, но счастливого будущего еще нет. Случился хороший, но проприетарный протокол EIGRP, разработанный Cisco.
В момент инициализации, любой узел в топологии ведет себя как обычный DV т.е проворачивает вычисления как это делает, например, Беллман-Форд.
Для работы DUAL нужно ввести некоторые новые сущности, а именно:
- RD(Reported distance) - метрика до удаленного узла
- CD(Computed distance) - посчитанная локальная метрика
- FD(Feasible distance) - самая выгодная посчитанная локальная метрика не может увеличиваться без участия DUAL в течении некоторой стабильной работы сети (до момента, пока не обнулится, скажем так).
Простыми словами, FD это самый выгодный CD.
- S(Successor) - сосед, имеющий наименьший FD до узла
- FS(Feasible successor) - соседний маршрутизатор, маршрут от которого гарантированно loop-free
Для отбора S и FS нужен некий арбитр - каждый маршрут проходит на соответствие условию FС (Feasibility Condition). Условие выглядит так: Feasibility Condition = Reported Distance < Feasible Distance т.е метрика RD, полученная от соседа, должна быть меньше FD на маршрутизаторе, который получил данный анонс.
Результат проверки на соответствие условию может быть одним из следующих вариантов:
- если RD < FD, путь считается loop free и выбирается FS
- если RD > FD, путь считается loop и FS никогда не станет
- если варианты закончились, путь, посчитанный ранее как loop, может перезапросить информацию о доступности узла (запустить алгоритм DUAL) и в случае положительного результата, будет выбран как Successor
Весь сакральный смысл работы DUAL заключается в проверке любого пришедшего маршрута на соответствие условию FC, что дает нам loop-free топологию без затрат ресурсов и знаний о всей топологии сети.
Подробнее уже посмотрим, когда доберемся до EIGRP.
Path vector
Path vector (PV) отличается от маршрутизации DV и LS. Тут каждая запись в таблице маршрутизации содержит сеть назначения, следующий маршрутизатор и путь к месту назначения.
BGP являет единственным ныне живущим членом семейства PV. BGP не выбирает кратчайший путь. Или самый быстрый путь. Или путь с наибольшей пропускной способностью.
Он действует очень похоже на DV, но разница в том, что вместо того, чтобы смотреть на расстояние для определения наилучшего пути без петель, он смотрит на различные атрибуты BGP.
BGP может манипулировать маршрутами с помощью различных атрибутов:
- AS_PATH
- Next-hop
- Origin
- local preference
- weight (для Cisco)
Если вы не укажете свои политики, BGP выберет кратчайший путь AS - это основной атрибут BGP. Выглядит это как строка из значений AS - 65000,65500,65501,65502
Но помните, это не означает наименьшее количество километров на поверхности планеты, наименьшее количество километров проводов или даже наименьшее количество маршрутизатора. Прагматически оказывается, что это путь с наименьшим количеством интернет-провайдеров, что может быть, а может и не быть тем, что вам нужно. В том числе из подобной свободы в 2000-х бушевали пиринговые войны :)
Короче говоря, BGP может выбирать практически любой путь, который он получает, как лучший. В основном это зависит от того, что было реализовано на уровне политик и что хочет сделать сетевой инженер.
Основной способ защиты от петель в BGP - список AS в AS_PATH. Анонс, проходя через маршрутизатор (для eBGP) добавляется номер каждой AS в список AS_PATH. Если маршрутизатор видит номер своей AS в AS_PATH, такой анонс дропается.
В iBGP AS_PATH не меняется, поэтому от петель защищает уже известный механизм - Split Horizon.
Вынырнули. На этом закончим с алгоритмами. Если я где-то ошибся, не стесняйтесь окунуть меня обратно.

Path Selection
Мы уже касались этой темы, но тут закрепим окончательно и перейдем к уже к конкретным протоколам.
Есть три сущности, влияющие на маршрутизацию пакета и установку нужных префиксов в RIB.
- Длина префикса (Prefix Length) - как известно, представляет из себя 32-битную маску подсети
- Административная дистанция (Administrative distance) - если по длине префикса несколько маршрутов совпадают, проверяется AD, что является некоторой метрикой надежности того или иного протокола, от которого получен маршрут
- Метрики (Metric) - если совпадают два предыдущих параметра, в дело вступают метрики конкретных протоколов
Вас может настигнуть некоторая путаница т.к в некоторых популярных ресурсах указан непривычный порядок описанных сущностей, а именно AD > Metric > LPM.
Почему так? Все дело в точке зрения на вопрос, с какого момента рассматривать процесс маршрутизации.
Порядок LPM > AD > Metric, более привычный, например мне, имеет смысл, когда на маршрутизатор приходит пакет и мы пытаемся определить, куда его отправить по уже сформированной таблице RIB. Грубо говоря, мы уже подразумеваем, что некоторые сети там присутствуют, остается только выбрать, куда отправить.
Порядок AD > Metric > LPM же берет начало от ситуации, когда в RIB еще нет маршрутов. Т.е сначала нужно решить задачу инсталляции маршрутов в RIB. А это значит, что нужно понять, какой протокол выиграет это соревнование в рамках AD и Metric, если AD совпадет.
В таком порядке, действительно, в RIB инсталлируются те маршруты, которые меньше по AD, остальные останутся в локальных таблицах своих процессов. Или, например, static роут с бОльшим AD, чем у основного, станет float-роутом, если, по какой-то причине, будет недоступен основной маршрут.
Если AD совпадают, то проверяются метрики протоколов, а уже после, когда маршруты попадут в RIB, на маршрутизатор придет пакет и затребует маршрутизацию. Вот с этого момента начнет работать порядок LPM > AD > Metric.
Prefix length
Да, вы уже это знаете, вопрос длины префикса решает Longest Prefix Match (LPM). Предписывающий, буквально, отправить трафик в ту сеть, у которой маска подсети больше т.е 10.0.1.0/28 будет приоритетней, чем 10.0.1.0/24.
Если есть несколько сетей с одинаковой маской, маршрутизатор переходит к сравнению административной дистанции.
Administrative distance
Каждый протокол маршрутизации (включая directly connected сети) имеет параметр “надежности”, выраженные в виде числа и названный administrative distance (AD).
Допустим, пришли к маршрутизатору несколько сетей с разными префиксами:
- EIGRP: 10.0.0.0/26
- RIP: 10.0.0.0/24
- OSPF: 10.0.0.0/19
- Static: 10.0.0.0/24
Какие сети будут установлены в RIB?
Эти маршруты лучшие для своих источников, следовательно мы смотрим на их AD в табличке:
| Routing protocol | AD |
|---|---|
| Connected | 0 |
| Static | 1 |
| EIGRP summary route | 5 |
| External BGP (eBGP) | 20 |
| EIGRP (internal) | 90 |
| OSPF | 110 |
| IS-IS | 115 |
| RIP | 120 |
| EIGRP (external) | 170 |
| Internal BGP (iBGP) | 200 |
| NHRP | 250 |
| Unknown/Not valid | 255 |
Как движок маршрутизации будет разбираться, какой маршрут добавить в RIB?
- если маршрута ранее не существовало, маршрут будет принят:
- если одинаковый маршрут пришел от разных протоколов, проверяется AD, в таблицу попадает маршрут с наименьшим значением AD
- если одинаковый маршрут пришел от одного протокола, например два static маршрута, AD совпадает и будет сверяться их метрика, в таблицу попадет маршрут с наименьшей метрикой
- если маршрут есть в RIB, сравнивается AD:
- если AD текущего маршрута ниже чем у маршрута-кандидата, маршрут откланяется. Затем уведомляется процесс, который этот маршрут предоставил.
- если AD текущего маршрута выше, то текущий маршрут удаляется из RIB, с последующим уведомлением процесса маршрутизации, ответственного за удаленный маршрут.
Основываясь на правилах выше, решим нашу небольшую задачку: RIP проигрывает соревнование проинсталлировать идентичную сетку 10.0.0.0/24, т.к то же самое пытается сделать и static. AD RIP = 120, а AD static = 1. Отсюда следует, что 10.0.0.0/24 попадет в RIB от Static маршрута.
OSPF и EIGRP не будут конкурировать между собой т.к предлагают разные сети, все они попадут в RIB, а выбор между ними, когда нужно будет маршрутизировать пакет, уже будет происходить в порядке LPM > AD > Metric. Следовательно 10.0.0.0/19 от OSPF и 10.0.0.0/26 от EIGRP попадут в RIB.
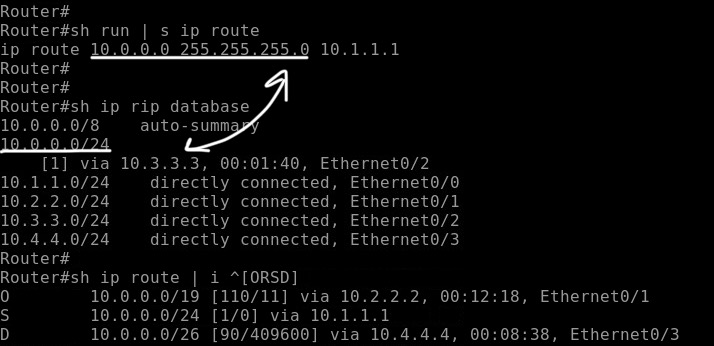
картинка честно украдена у Михаила, с сайта lubnfun. Пример взят оттуда же, там чуть больше конкретики.
AD не прибита гвоздями, ее можно изменить, при очень острой необходимости. Но удостоверьтесь, что вам оно действительно надо.
Metrics
Вопрос метрики достаточно широк т.к охватывает собой все разнообразие ее представления в различных протоколах маршрутизации.
Что мы точно можем утверждать - метрика проверяется в рамках одного протокола маршрутизации и следует принципу “меньше > лучше”.
Так же мы знаем, что считается метрикой в каждом из протоколов:
RIP - hop count
EIGRP - Composite Metrics (BW, Delay, Load, Reliability, MTU)
OSPF/ISIS - cost (на основе BW интерфейса)
BGP - attributes
Более детально метрики разбирать имеет смысл при рассмотрении каждого из протоколов, поэтому пока опустим эту часть. О чем точно стоит упомянуть, что произойдет, если метрика так же совпадет? Произойдет балансировка по Equal Cost Multi-Path или ECMP.
Буквально, в RIB появляется два равноправных маршрута, трафик по которым балансируется per flow (по умолчанию), чтобы гарантированно пакеты от одного сервиса шли одним путем, а не как попало.
Протокол должен уметь в ECMP - Static маршруты, RIP, EIGRP, OSPF и IS-IS его поддерживают.
EIGRP позволяет делать Unequal-Cost Load Balancing (UCMP) - эта возможность доступна, но не включена по умолчанию. Этот механизм позволяет балансировать трафик по маршрутам с неравнозначной метрикой, ваш Кэп.
Балансировка - это отдельная большая тема, которую я трогал издалека и с опаской. Было дело, на первых собесах сыпался именно на ней, поэтому победить эту тему - дело принципа :) К ней мы еще вернемся.
Sources
- CISCO EIGRP DUAL Algorithm
- About BGP best path
- Loop-Free Routing Using Diffusing Computations (см. ЯД)
- Comparison of RIP, OSPF and EIGRP Routing Protocols based on Riverbed (см. ЯД)
- Termination detection for diffusing computations (см. ЯД)
- RFC 7868 - EIGRP
- RFC 2453 - RIP version 2
- RFC 4271 - BGPv4
- RFC 1583 - OSPFv2
Напомню, я собираю все материалы по ENCOR в одном месте.
Источники, имеющие пометку (см. ЯД) можно найти по ссылке.
Хочешь обсудить тему?
С вопросами, комментариями и/или замечаниями, приходи в чат или подписывайся на канал.